Implementing the Alphazero Method for Connect 4. Part 2: The Neural Network
Last week we talked about various tree search techniques, and in particular how tree search methods can be improved two ways:
- Having a method to heuristically determine which moves are promising before searching the tree
- Having a strong and/or efficient evaluation function which tells us if the board state is advantagous
Alphazero implements both of these with a neural network.
Neural Networks
Our goal is to find an approximation for the function,
\[y = f(x),\]where \(x\) is the board state, and \(y\) is something containing information on both which moves are promising and the evaluation. A neural network is one way we can attempt to make this approximation.
Fundamentally a neural network is made up of a set of connected neurons which are often grouped into layers
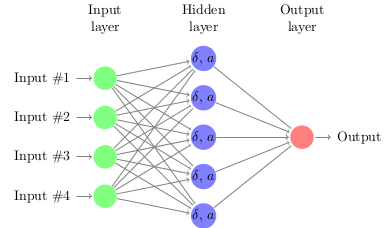
Every connection has a weight associated with it, \(w\), while every neuron has a value, \(\delta\), and what is known as an activation function, \(a\). The value of any neuron can be calculated by summing over all connections in the layer previous to it,
\[\delta = a\left(\sum_i \delta_i w_i\right).\]Without the activation function every operation would be linear, and our neural network would only be able to approximate linear functions. If the activation function is non-linear then the neural network can approximate non-linear behavior. The most common activation function used is the Rectifier Linear Unit (ReLU) function,
\[relu(x) = \begin{cases} 0 & x\leq 0 \\ x & x > 0 \\ \end{cases}\]The ReLU function is commonly used because it is simple and allows efficient calculation of derivatives.
Neural networks are broken into layers, our network above has three layers: input, output, and a hidden layer. A layer is referred to as hidden if it is not directly connected to the input or output values. Furthermore, layers are often given names based upon how it is connected to the previous layer. Our hidden layer above is known as a dense layer because every neuron is connected to every one in the previous layer. Another option is a convolutional layer where neurons are only connected to a few in the previous layer that are locally close to it. Naturally dense layers will have considerably more weights than convolutional layers which means that they can approximate more complicated functions, but remember we determine what these weights are which could be a problem if we have too many.
The word “deep” in neural networks refers to how many hidden layers are present. A typical deep neural network would be written something like this
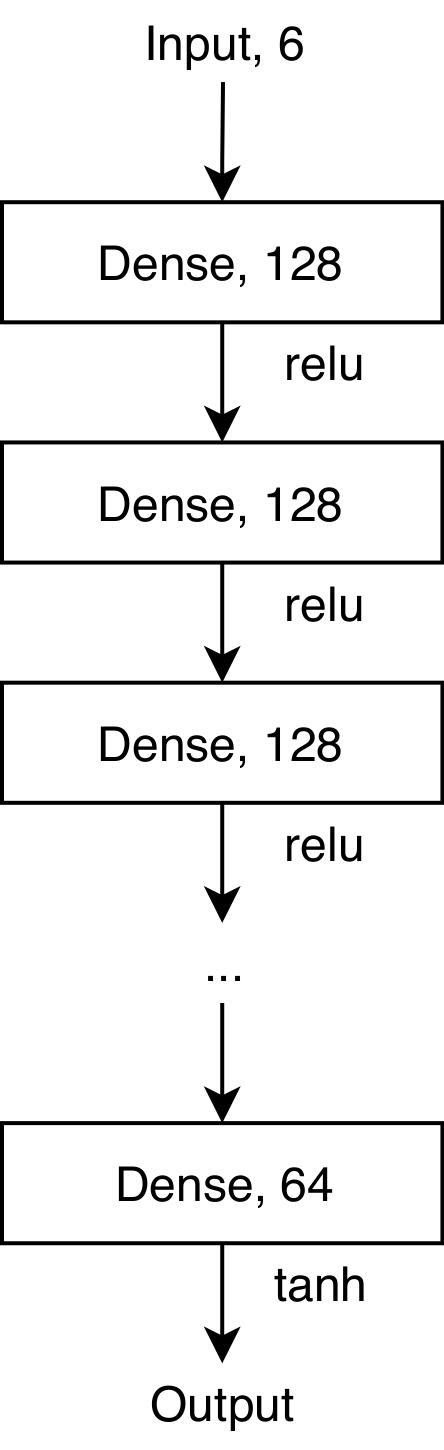
The deeper the network the more complicated of function it can approximate, but it may be harder to find the ideal weight values. It was found that this problem can be greatly helped by using what is known as a residual neural network.
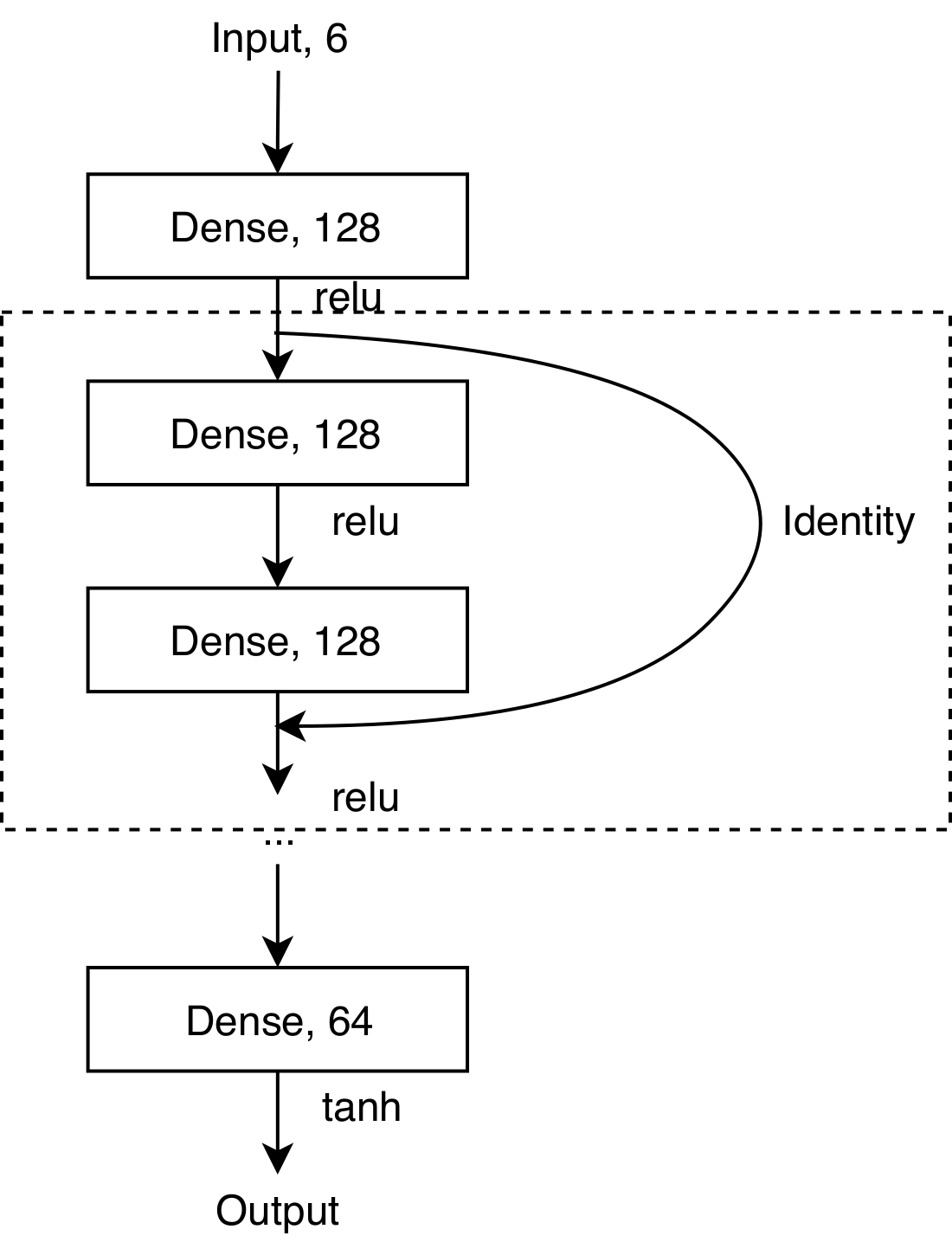
Here an identity connection is added in-between layers. With the identity connection each layer only needs to add additional information, it does not need to re-learn information that is already there.
The neural network used by Alphazero is deep residual neural network that has two output structures.
- The policy output. Every possible move is assigned a value between 0 and 1 which estimates the probability of the move being played. This is our heuristic which helps us focus in the tree search.
- The value output. A number between -1 and 1 to estimate how advantageous the board state is. 1 would be the game is won, -1 the game is lost, 0 the game is drawn.
Training the Network
We have constructed the neural network, but we still have to determine the value of the weights. For now, let us assume we have a set of input values \(x\) and output values \(y\) which satisfy the function we are trying to approximate \(y = f(x)\) (more on how we get these values later). Our goal is to find the set of weights \(w\) which minimize some cost function between the true values and our predicted values. In the case of Alphazero the cost function used is cross entropy for the policy predictions, and mean squared error for the value predictions. We can write this cost function as a function of the input values and the weights, \(\chi^2(w; x)\)
One standard way of minimizing any function is through gradient descent, roughly, we iterate through,
\[w_i = w_{i-1} - \nabla \chi^2(w; x)\]where \(\nabla \chi^2(w; x)\) is the gradient of the cost function with respect to the weights.
Most (all) software packages that implement neural networks will also implement what is known as backpropagation.
Backpropagation is an efficient method to calculate this gradient using ideas similar to auto-differentiation.
However, when we have a large amount of data standard gradient descent is unfeasible due to the large amount of memory that would be required for the gradient.
The most common method of training is Stochastic Gradient Descent (SGD). SGD is very similar to standard gradient descent, except instead of working with the entire dataset at a time we work with smaller batches.
Self Play
Our method of training before assumed we had a set of values \(y\) and \(x\) that were taken from the function we are trying to approximate. How do we get these? Something that has been done in the past was looking at databases of professional games, the neural network could then be trained to approximate these games. However Alphazero takes another approach, one that uses no human information. It simply plays against itself.
In the beginning, all of the neural network weights are initialized randomly. The network effectively predicts random values, that have nothing to do with the game. Alphazero then plays thousands of games against itself, at every move the board state, the move played, and the eventual winner of the game is recorded. The games played are of terrible quality, only slightly better than random because of the tree search that is done.
The network is then trained using the results of these almost random games. Since the quality of the games is so poor, the network does not learn very much, but it does learn something. Then, thousands more games are played using this new network, which produce slightly higher quality games. The process is repeated repeatedly training and playing against itself.
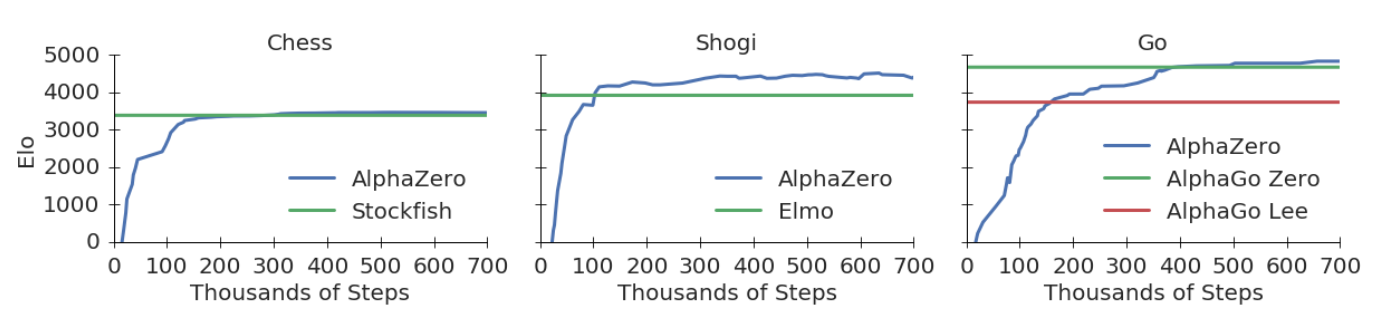
The above figure is from the Alphazero paper (https://arxiv.org/pdf/1712.01815.pdf) which shows how the program becomes stronger through self play.
The next post will outline my efforts to apply these techniques to connect 4.