Implementing the Alphazero Method for Connect 4. Part 1: Tree Search
AlphaGo Zero was first published in Nature in October 2017. At the time I was fascinated with the technique and tried to learn as much as I could about it. I quickly decided that the best way to truly understand how AlphaZero worked was to try to implement it myself. Obviously an exact replica of AlphaGo Zero is not possible on consumer hardware (but I encourage anyone interested in a community effort to check out LeelaZero). Therefore I decided to try to implement the AlphaZero technique to a simple, solved game, connect 4.
I plan to split this endeavor into three parts:
- Monte Carlo tree search, specifically the upper confidence bound applied to trees (UCT) variant
- The AlphaZero policy and value network, and how it is learned through self play
- Results in applying the method to connect 4
The Game Tree
Any two player game where the players alternate taking turns can be represented as a tree
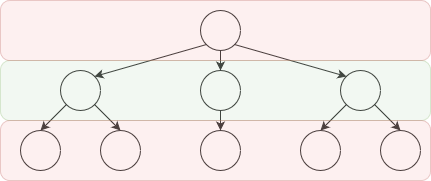
In the game tree each node represents a game state while every edge is a move that can be played. This game tree is for a two player game, where each players move is shown by red or green. Terminal nodes of the game tree are game positions where the game is over, and we can assign either win, draw, or loss.
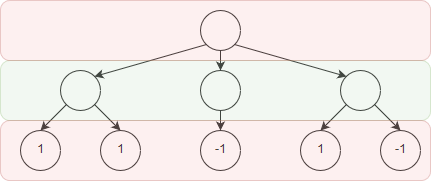
Where we have labelled a win with the value 1, a loss with -1, and a draw with 0. The goal when playing the game is to best possible move on every turn. To find the best possible move we can propagate the values at the terminal node up. Looking at the tree above, we can see that if we make the move on the left, no matter what we end up winning. Formally this is shown by the minimax principle which states that each player should “minimize the maximum losses that could occur”, which sounds quite complicated. When looking at the game tree however it is a relatively simple concept.
On our opponents turn, we should propagate the evaluation upwards by taking the minimum value.
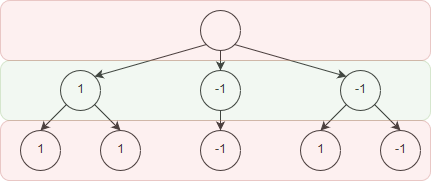
This simply means that our opponent will play the best possible move, the move which gives us the lowest evaluation.
And on our turn, we should propagate the values upwards by taking the maximum, since we are going to play the best possible move for us.
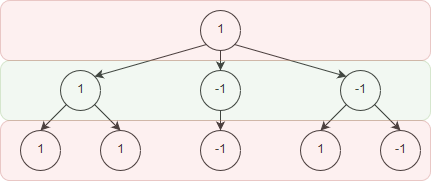
Therefore this position should be a win for us, if we play perfectly. Propagating the game tree using the minimax principle can be done as long as we know the full game tree. However for many games it is too computationally intensive to write out the full game tree and we need to make some kind of approximation. In fact, any game where we can write out the full game tree starting from the first move would by definition be a solved game.
Searching the Game Tree in Chess
Chess has been one of the largest successes in AI ever since deep blue defeated Kasparov. Today a chess engine on any cell phone is considerably stronger than the strongest professional players.
The basis for any chess AI is searching the game tree, however, there are too many moves to search through which means we have to stop before reaching a terminal state. Since we don’t have a terminal state we can’t assign our convenient values of 1 for a win, -1 for a loss, 0 for a draw. Instead, at the position we stop we need some function that approximates how good that position is for us. In chess, a simple evaluation function counts how many pieces each player has, assigning a weighted point value (e.g. 1 for a pawn, 5 for a rook, …). This turns out to be a relatively good approximation for determining which player is ahead, generally the player with better pieces is winning in chess. These evaluation numbers can then be propagated back up to the root node using the same minimax principle.
Without going into much details, the actual tree search methods used by modern chess engines employ many advanced techniques to speed up the search. Some of the more important ones are
- Alpha beta pruning, parts of the tree that can be proven to be disadvantagous to the player can be discarded and not searched
- Many types of heuristics, which can go hand to hand with alpha beta pruning. Knowing what parts of the tree are worth exploring first can greatly increase the depth can be achieved.
- More advanced evaluation functions. If you have a perfect evaluation function you only need to search 1 move deep, because it will tell you what move is best. A great evaluation function that only looks 5 moves ahead could be considerably better than a poor one that is able to move 10 moves ahead. Note that the evaluation function has to be evaluated at every end node, of which there are likely millions, therefore it must be computationally efficient.
Searching the Game Tree in Go
Traditionally applying the same methods used in a game like chess have not been very successful in go. There are two reasons for this:
- The game tree for go is much bigger. This is because of what is known as the branching factor. Every move in go there are ~200 possible moves, compared to ~30 for chess. Since the game tree grows exponentially with this number, it is considerably harder to search for.
- There is no good, computationally efficient, evaluation function for go.
The first reason is often cited as the primary limitation of brute force tree searching methods for go, however I feel that the second reason is perhaps more important and often overlooked. In chess there is a simple evaluation function that works quite well, how many pieces and how good those pieces are. In go the act of counting territory is quite complicated, there are unresolved fights all around the board, life and death of groups need to be considered, determining who is winning a go game in the middle of the game is very difficult even for professional players. Because of these two limitations programs which used classical search methods are barely able to beat beginners of the game.
The Solution? Monte Carlo Tree Search
We can’t evaluate game states in the middle of the game, but at the end we can decide who the winner was. How do we get to the end of the game without evaluating the full game tree? Monte carlo tree search.
The basic idea is we continuously play random moves for each player until we reach the end of the game, which we can evaluate. We do this thousands of times for each position, the result of these playouts can be used to evaluate the game state. In the limit of unlimited playouts this would be equivalent to writing down the entire game tree and solving the game.
If you read through the idea for Monte carlo tree search and thought it was ridiculous, you would not be alone. However these methods when applied to go were able to create AI’s that were at the strong amateur player level, considerably better than the best classical tree search programs.
Naturally there are a variety of techniques that can improve raw monte carlo tree search, the most popular method is known as Upper Confidence bound applied to Trees (UCT). The general idea is that a move that has a very high win rate should be explored further, either to cement it as a good move, or to prove that the opponent has a counter move that makes the move unreasonable. Furthermore, moves we should give some additional weight to moves that we haven’t explored at all yet. For both of these reasons UCT chooses moves in a weighted random fashion, focusing in on important parts of the game tree.
Because UCT is a Monte carlo search, generally it has had trouble scaling (since Monte carlo methods usually scale with the square root of the number of samples). Modern go AI’s would include a UCT search, perhaps combined with a large number of heuristics, maybe a classical search methods for life and death, and an amalgamation of a large number of techniques.
The AlphaZero Tree Search
Let us recall the two problems with tree search in go:
- There are a large number of moves to consider
- Evaluating the game state is hard
AlphaZero solves both of these problems with a neural network. The inputs to the neural network are the game state, and the neural network outputs two things
- The policy. A weighting given to each possible move based on how good it is expected to be.
- The evaluation.
If both of these quantities are good, then most of our tree search problems are solved. We would not have to search through the full tree because the policy would let us hone our search on moves that have the possibility of good. And having a good evaluation is self explanatory.
The natural tree search method to use with the neural network is the UCT method described above. The UCT search can be guided by the policy, and having a good evaluation function means that we can stop in the middle of the tree, we do not have to randomly play until the very end of the game.
Part 2 will focus on how this neural network is constructed and trained.